Functional programming 101

Functional programming is a programming paradigm, where programs are a composition of pure functions. This represents a fundamental difference to object-oriented programming, where programs are sequences of statements, usually operating in a mutable state. These are organized into so-called functions, but they are not functions in the mathematical sense, because they do not meet some fundamental characteristics.

Firstly, a function must be total, this means that for each input that is provided to the function there must be a defined output. For example, the following function dividing two integers is not total:

def divide(a: Int, b: Int): Int = a / b

To answer why this function is not total, consider what will happen if we try to divide by zero:

divide(5, 0)


// java.lang.ArithmeticException: / by zero

The division by zero is undefined and Java handles this by throwing an exception. That means the divide function is not total because it does not return any output in the case where b = 0.

Some important things we can highlight here:

• If we look at the signature of this function, we realize that it’s telling a lie: that for each pair of integers a and b, this function will always return another integer, which we have already seen is not true for all cases.
• This means that every time we call the divide function in some part of our application we will have to be very careful, as we can never be completely sure that the function is going to return an integer.
• If we forget to consider the unhandled case when calling divide, then at runtime our application will throw exceptions and stop working as expected. Unfortunately, the compiler is not able to do anything to help us to avoid this type of situation, this code will compile and we will only see the problems at runtime.

So how can we fix this problem? Let’s look at this alternative definition of the divide function:

def divide(a: Int, b: Int): Option[Int] =
  if (b != 0) Some(a / b) else None

In this case, the divide function returns Option[Int] instead of Int, so that when b = 0, the function returns None instead of throwing an exception. This is how we have transformed a partial function into a total function, and thanks to this we have some benefits:

• The function’s signature is clearly communicating that some inputs are not being handled because it returns an Option[Int].
• When we call the divide function in some part of our application, the compiler will force us to consider the case in which the result is not defined. If we don’t, it will be a compile-time error, which means the compiler can help us to avoid many bugs, and they will not appear at runtime.

The second characteristic of a function is that it must be deterministic and must depend only on its inputs.  This means that for each input that is provided to the function, the same output must be returned, no matter how many times the function is called. For example, the following function for generating random integers is not deterministic:

def generateRandomInt(): Int = (new scala.util.Random).nextInt

To demonstrate why this function is not deterministic, let’s consider what happens the first time we call the function:

generateRandomInt() // Result: -272770531

And then, what happens when we call the function again:

generateRandomInt() // Result: 217937820

We get different results! Clearly this function is not deterministic and its signature is misleading again, because it suggests that it does not depend on any input to produce an output, whereas in truth there is actually a hidden dependency on a scala.util.Random object. This may cause problems, because we can never really be sure how the generateRandomInt function is going to behave, making it difficult to test.

Now, let’s have a look at an alternative definition. For this, we’ll use a custom random number generator, based on an example from the Functional Programming in Scala book:

final case class RNG(seed: Long) {
  def nextInt: (Int, RNG) = {
    val newSeed = (seed * 0x5DEECE66DL + 0xBL) & 0xFFFFFFFFFFFFL
    val nextRNG = RNG(newSeed)
    val n       = (newSeed >>> 16).toInt
    (n, nextRNG)
  }
}

def generateRandomInt(random: RNG): (Int, RNG) = random.nextInt

This new version of the generateRandomInt function is deterministic: no matter how many times it is called, we will always get the same output for the same input and the signature now clearly states the dependency on the random variable. For example:

val random        = RNG(10)
val (n1, random1) = generateRandomInt(random) // n1 = 3847489, random1 = RNG(252149039181)
val (n2, random2) = generateRandomInt(random) // n2 = 3847489, random2 = RNG(252149039181)

If we want to generate a new integer, we must provide a different input:

val (n3, random3) = generateRandomInt(random2) // n3 = 1334288366, random3 = RNG(87443922374356)

Finally, a function must not have any side effects. Some examples of side effects are the following:

• memory mutations,
• interactions with the outside world, such as:
  • printing messages to the console,
  • calling an external API,
  • querying a database.

This means that a pure function can only work with immutable values ​​and can only return an output for a corresponding input, nothing else.

For example, the following increment function is not pure because it works with a mutable variable a:

var a = 0;
def increment(inc: Int): Int = {
  a + = inc
  a
}

And the following function is not pure either because it prints a message in the console:

def add(a: Int, b: Int): Int = {
  println(s "Adding two integers: $ a and $ b")
  a + b
}

The following table summarizes the major differences between these two programming paradigms:

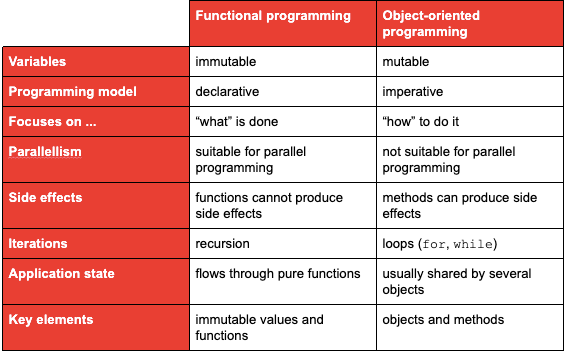
For various reasons, functional programming may still seem complex to many. But, if we take a closer look at the  benefits, we can change our way of thinking.

For starters, embracing this programming paradigm helps us to break each application down into smaller, simpler pieces that are reliable and easy to understand. This is because a functional source code is often more concise, predictable, and easier to test. But how can we ensure this?

• Since pure functions do not rely on any state and instead depend only on their inputs, they are much easier to understand. That is, to understand what a function does, we do not need to look for other parts of the code that could affect its operation. This is known as local reasoning.
• Their code tends to be more concise, which results in fewer bugs.
• The process of testing and debugging becomes much easier with functions ​​that only receive input data and produce output.
• Since pure functions are deterministic, applications behave more predictably.
• Functional programming allows us to write correct parallel programs, since there is no possibility of having a mutable state, therefore it is impossible for typical concurrency problems to occur, such as race conditions.

Since Scala supports the functional programming paradigm, these benefits also apply to the language itself. As a result, more and more companies are using Scala, including giants such as  LinkedIn, Twitter, and Netflix. In addition, this year Scala is one of the top 10 languages ​​that developers want to learn.