Optics beyond Lenses with Monocle

If you are a Scala developer for some time you are probably familiar with the concept of Lenses. It got a lot of traction in the community as it resolves the very common problem of modifying deeply nested case classes. But what is not that universally known is that there are more similar abstractions. They are usually referred to as Optics.

In this post, I will try to present some of them and give some intuition on what are possible applications for them. This article is focused more on the applications rather than on mathematical foundations. Moreover, it attempts to highlight that idea of Optics goes much, much further than the manipulation of nested records.

In this post, I will use code and terminology taken from Monocle – Scala library for Optics. Quoting its documentation:

Optics are a group of purely functional abstractions to manipulate (get, set, modify, …) immutable objects.

All illustratory code used in this article may be found in accompanying repo.

Short Lens recap

If you are familiar with Lenses you can skip to other usages of Lenses.

What is Lens

Lens in essence is a pair of functions:

• get(s: S): A
• set(a: A): S => S

What are S and A? S represents the Product (or in other words “the whole part”, or container) and A some element inside of S (or in other words “the specific part”). It’s good to keep in mind that naming convention as it is omnipresent in Monocle and literature about Lenses. It will be used in the rest of the article.

In a nutshell – having get Lens allows to “zoom in” into a specific part of Product and by having set lets you construct a new “whole-part” with an updated “specific part”. After zooming in we lose some information and that’s why setneeds S as an argument – to be able to reconstruct the whole Product.

Very simple example with Monocle

Before using Lens we need to … create one. With Monocle it boils down to calling Lens.apply method. It takes two arguments, first one is get function and the second one is set function:

The above code is everything you need to create Lens. Mind that not every pair of functions that was created with Lens.apply is a real Lens. Such pair must also obey Lens laws – the same way as not every class with a proper signature of flatMap method is a lawful Monad. For brevity I do not include those laws here, they can be found e.g. in scalaz tutorial. We will get back to them in section about testing.

Let’s see what we can do with nameLens:

Not very impressive but note that based on those primitive operations Lens has defined some other operations. An example of such an operation is modify which allows to setting new value of specific part based on its previous value:

You may think: “So what? We can get and set case class values in some new way – what’s the point?”. The true benefit of Lenses lies in their composability.

Composition of Lenses – the classic example

To illustrate the composition of Lenses I will use classic example (as in e.g. Ilan Godik’s talk):

Full code for this example.

Let’s say that having Person the instance you want to turn its street’s name to upper case. The most straightforward approach is very lengthy:

With Lenses same code may look like this:

As you can see the code is shorter and more readable. As Ilan noticed code size grows quadratically with a straightforward approach and linearly with Lenses.

Another interesting way of thinking about Lenses is that they help you to lift functions A => A to S => S. In our case, we can lift the function String => String (as the street name is a String) to Person => Person:

Other usages of Lens

The good thing about the above classic example is that it made developers aware of Lenses. On the other hand, it may have built an impression that Lenses, and Optics in general, are “just a thing that helps in accessing nested case classes”.

However, the true power of Optics lies in the fact that there are more of them and they’re fully composable. But even with sole Lenses you can do much more than accessing nested records. You can use them for having “virtual fields”, maintaining invariants or accessing bit fields.

Lens Generation

In case of Lenses specialized in accessing case class fields, their code can be generated automatically most of the time.

What is Prism

Prism is essentially a pair of functions:

• getOption: S => Option[A]
• reverseGet: A => S

where S represents the Sum (also known as Coproduct) and A is a specific part of the Sum. Based on those definitions we may see that Prism is “Lens for trait hierarchies”. While it clearly does not drain the essence of Prism and we move beyond that, it gives you nice intuition to start with.

It also explains why Prism’s getOptional (counterpart of Lens get) returns Option – that’s because “zooming in” to a particular subtype may fail. That’s in lucid opposition to Lens get which may never fail – Product always contains all its parts.

What does reverseGet reveal about the nature of Prism? That is a counterpart of Lens set: A => S => S ¹, but it does not have S as an argument. That is not needed because in the case of Prism, the specific case holds the whole information needed to produce a more general Sum.

Simple example with sealed trait hierarchy

Let’s take such a sealed trait hierarchy (it’s a way to express Sum type in Scala, full code):

Let’s define Prism[Json, String]:

Now we can try out primitive operations:

Let’s make getOption fail with non-JStr input:

OK, I admit that those examples were not very exciting. Let’s do something more useful with derived combinators. Let’s try to rewrite such code:

Same code with Prism:

Mind the clarity of revealing the intention in the above code. Also, thanks to the partial application we can lift the function String => String to Json => Json:

modify brings another matter on the surface – what if Json on input is not “focusable” by given Prism? Let’s try:

As you see we got original value back. It may be ok in some cases but if you need information about success of operation you need to use modifyOption instead:

Prism generation

Prisms also can be generated for simple cases.

Prism as a safe downcasting

In this section, we will try to write access and modification code for operating on String as an Int. Since treating String as Int (with e.g. String.toInt) may fail it seems like a good use case for Prism. Let’s start with defining Prism[String, Int] (full code):

It’s not a lawful Prism but let’s ignore it for a while (we’ll get back to this in testing section).

We can also lift functions Int => Int to String => String:

Prism composition

As an example in this section we will use another case class – Percent. It uses Int from inclusive range 0-100 as its internal representation. It is defined as follows:

Given Percent.fromInt method it’s easy to implement Prism[Int, Percent]:

Let’s say we want to define Prism[String, Percent]. As Prism is composable we can do that just by simply composing Prism[String, Int] and Prism[Int, Percent]:

You may be surprised by PPrism – it will be described later. For now, all you need to know is that stringToPercent type is the exact equivalent of Prism[String, Percent].

This is how the composed prism behaves:

Testing Prisms (and Optics in general)

Remember when I said that our prism was not lawful? This section will explain it more in detail.

In the same way, as we define concrete instances of most of the functional abstractions (e.g. Monads) we construct Prisms (and other Optics) instances by:

• implementing methods needed by API
• ensuring laws are obeyed

The former one is easy as the compiler does the verification if signatures follow API. However, the compiler is not able to verify if laws are obeyed. Therefore we need to take care of that by writing proper tests.

To verify that created Prism follows Prism laws we will use monocle-law. That is an additional artifact published as part of monocle project. It’s built on top of scalacheck and Typelevel’s discipline and contains definitions of all Optics laws. monocle-law uses a property-based approach to testing.

In this approach, you define which properties should your code hold and then those properties are checked against randomly generated values. In the case of testing Monocle’s Optics we will use Optics laws as assertions. Therefore we just need to take care of generating input values.

To be more specific we will see how to implement tests for our Prisms:

As you can see, on high-level it seems very succinct. PrismsTests is defined by monocle-law and is responsible for creating runnable verification of Prism’s laws for given Prism. Then we are running it with checkLaws. You may wonder where is generating part. In that regard it’s helpful to take a look at PrismTests.apply method signature:

It says that compiler requires implicit instance of Arbitrary and Equal for both A and S. Arbitrary[S] is responsible for generating possible values of S and Equal is scalaz’s typeclass for equality checking. For us more interesting is Arbitrary. Scalacheck has instances of Arbitrary for basic types and there are suitable defaults for Int and String.

However, because instances of String generated by default generators are completely random we will create our own generator. Instead of completely randomized Strings would we would like to have mostly inputs similar to numeric values with some addition of different values. You may take a look at ArbitraryInstances to see how we define Arbitrary for String and Percent.

When I ran this test I saw:

Now we see that, as mentioned before, our stringToIntPrism is not a lawful Prism. In that case, it’s pretty easy to see what’s wrong – stringToIntPrism does not preserve some values during the round trip. To be more concrete:

Prism laws say that the expected result should be “005” instead. We can solve this problem by restricting acceptable String inputs. We can do this as follows:

Now tests are passing.

Laws definitions similar to PrismTests exists to all Optics (e.g. Lens). As you saw testing against those laws is pretty straightforward and really helpful to spot unlawful behaviors early.

Iso

You can think of Iso as something that is simultaneously Lens and Prism. That means that navigating from S and A is always successful (as in Lens) and navigating from A to S does not need any additional information besides of A value (as in Prism) – in other words transformation from S to A is lossless. As you probably already concluded this corresponds nicely with the mathematical concept of Isomorphism.

Therefore primitive operations for Iso are symmetrical:

• get: S => A
• reverseGet: A => S

When is Iso useful? Basically anytime when representing essentially the same data in different ways. One classic example is working with physical units. Let’s say we have two classes:

We can create an Iso and use it:

Optional

You may think of Optional as something more general than both Prism and Lens. Similarly to Prism, the element A we are trying to focus on may not exist. At the same time focusing is also lossy – after focus, we don’t have enough information to go back to S without additional argument. Those are primitive operations for Optional:

• getOption: S => Option[A]
• set: A => S => S

Let’s say we are working with the following class hierarchy (full code):

Let’s consider Optional[Error, String], which would allow us to “zoom into” detailedMessage. It cannot be Lens[Error, String] as ErrorB does not contain detailMessage. That’s why we need Optional – it explicitly tells us that the operation may fail.

Such Optional can be implemented like this:

It’s quite rare to see Optional implemented directly like above. Instead, usually you implement separate Prism and Lens and then compose them together. It will be discussed more in-depth later.

Hierarchy of Optics

We got familiar with 4 types of Optics. How they related to each other is depicted in the following diagram:

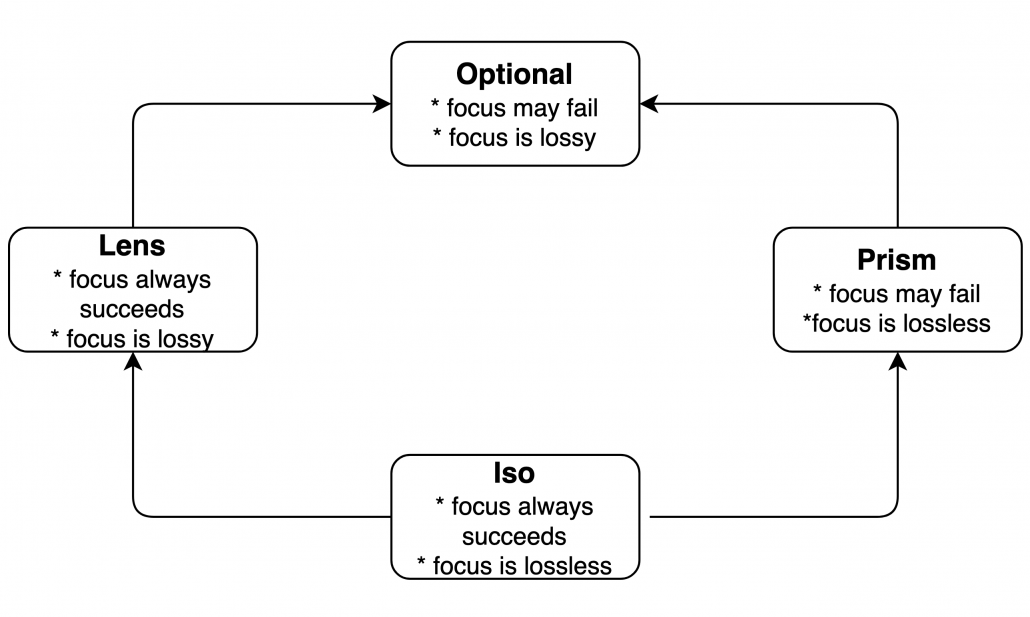
This diagram is meant to be read as a UML class hierarchy diagram, so e.g. arrow going from Lens to Optional means that Lens is a special case of Optional. And what does it mean that both Lens and Prism can be treated as Optional? Lens is an Optional for which getOption always succeeds. Prism is an Optional for which we ignore S (“the whole part”) – A (“the specific part”) holds all information to produce new S.

This is not a full list of Optics. Composition of different types of Optics

The composition of different types of Optics is what makes them especially appealing. It allows you to easily access and transform data between various representations. The beauty lies in the fact that you need to define only a small portion of Optics – the rest of them you can create by simply composing existing Optics.

Simple example

In one of the previous examples we had code similar to this:

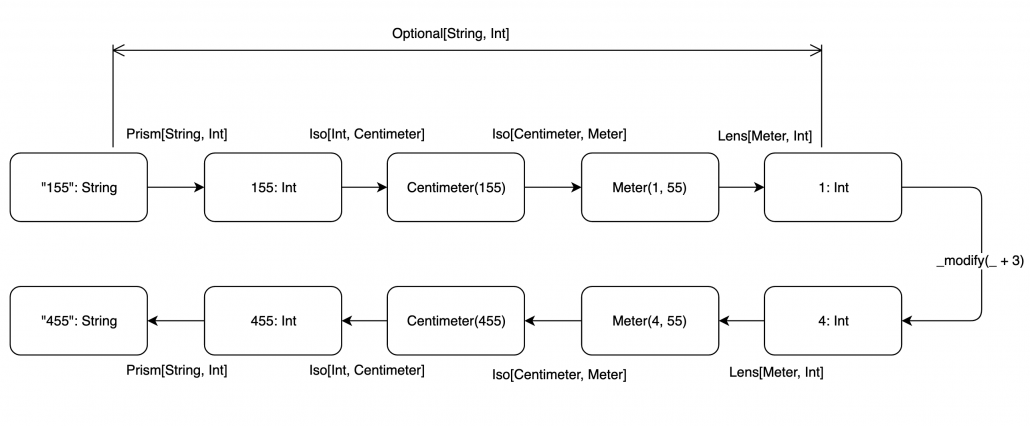
We are accessing m.whole just to update it and put it back to case class using copy. Sounds like a job for Lens. Also, instead of using Centimeter as input and output, we can use String together with Prism[String, Centimeter]. The last one may be not a good idea in general but in test code, it makes sense to strive for short and readable code. Having proper Optics declared, and composing them is a matter of:

The result of composing Prism, Iso and Lens is Optional. It makes sense as it is the nearest common ancestor of types being composed in Optics hierarchy. Resulting stringToWholeMeter may be used like this:

The following diagram is an attempt to visualize that flow:

Real-world example: circe-optics

circe-optics is an excellent real-world application of Optics idea. When you think a while about traversing and modifying JSON documents it may strike you that there are quite a few aspects common with Optics.

Field with a given name may or may not exist – sounds like Prism, we may lossily focus into some field and the notion of nesting – sounds like Lens, then we need to “assume” that some field is e.g. String – sound like Prism again. Let’s take a very short look at circe-optics implementation.

It defines Prisms for all JSON types as e.g.:

Since jsonNumber in turn, is Prism[Json, JsonNumber] it is a great example of a composition of the same types of Optics. Besides that, the library uses different types of composition in many places. A good example may be “zooming in” deeper into JSON structure. You can access {order: {address: {...} }} in a javascript-like way:

Nice “dot syntax” has been implemented with Dynamic (mentioned on our blog). Dynamic dispatches field-like accessors to the method selectDynamic, which does the following:

As we see it composes jsonObject Prism with index Optional. Our intuition says that it makes sense because before going deeper at desired field we need to “assume” with Prism that the current field is a JSON object.

All in all – we got a bunch of composable Optics – what can we do with them? Let’s say we want to modify a string field in some nested JSON. The non-optics solution may look like the following (full code):

Let’s compare it with the optics equivalent:

The difference in simplicity and conciseness is striking.

It was a very rough introduction to the internals of optics-circe. I encourage you to study source code – it’s a really elegant solution to a practical problem. Also, the codebase for optics is relatively small and contains nice tests.

Polymorphic Lenses

I owe you an explanation on PPrism. While toying around with Monocle you will quickly come across P-prefixed types like PPrism, POptional and PLens. In all those cases P stands for polymorphic. What is meant by some Optic being polymorphic? You may have noticed that all Lenses are pair of functions on types S and A. When Optic is polymorphic additional two types come into play for “reverse” operation: B for an argument and T for a result of that operation.

It may be easier to grasp this idea by looking at PLens definition:

Summary

• Monocle gives us a whole spectrum of Optics. This article describes just part of them
• Whenever you find it troublesome to traverse or modify deeply nested or recursive data structures it is a sign that Optics may help
• When you need to work with different representations of essentially the same data it is also a signal that Optics may be useful. It implies that all (de)-serialization code is a good candidates for Optics
• To gain full benefits of Optics they should be lawful
• Always test your instances of Optics against their laws. monocle-law is a way to go in Monocle

References

The first two references were my main inspirations for this article. I recommend watching both of them to get the essence of Optics. If you find them interesting enough to dive even deeper, you should explore further references.

Talks

• Ilan Godik’s talk – great introductory talk into Optics in Scala using Monocle by one of its maintainers. Short and does not require any specific knowledge upfront. Also introduces Van Laarhoven Lenses
• Julien Truffaut’s talk – Julien is the author of Monocle, in this talk, he provides a great overview and intuitions about various types of Optics
• another talk by Julien Truffaut – this one is about JsonPath – a concept already mentioned in this article in the section covering circe-optics
• Brian McKenna’s talk – Brian goes through Optics libraries in a few different languages: PureScript, Haskell, Scala and Java. Mentions nice examples of applications including representing web pages as Optics which allows navigating between state and UI in Halogen, working with Kinesis records in Haskell, handling errors with Prisms in Scala
• Simon Peyton Jones talk – a basic overview of Lenses in Haskell
• Bartosz Milewski’s class part 1 and part 2 – Bartosz explains Lenses from a Category Theory point of view

Other resources

• Accompanying repository with code being discussed in this article
• List of references from Monocle documentation
• Scala Exercises page
• goggles – the new kid on the Scala Optics block
• excellent compilation of different type of Optics by Oleg Grenrus. Haskell used for explanations
• lens over tea – a series of articles about Optics and its implementation in Haskell